Energy in Electricity Networks

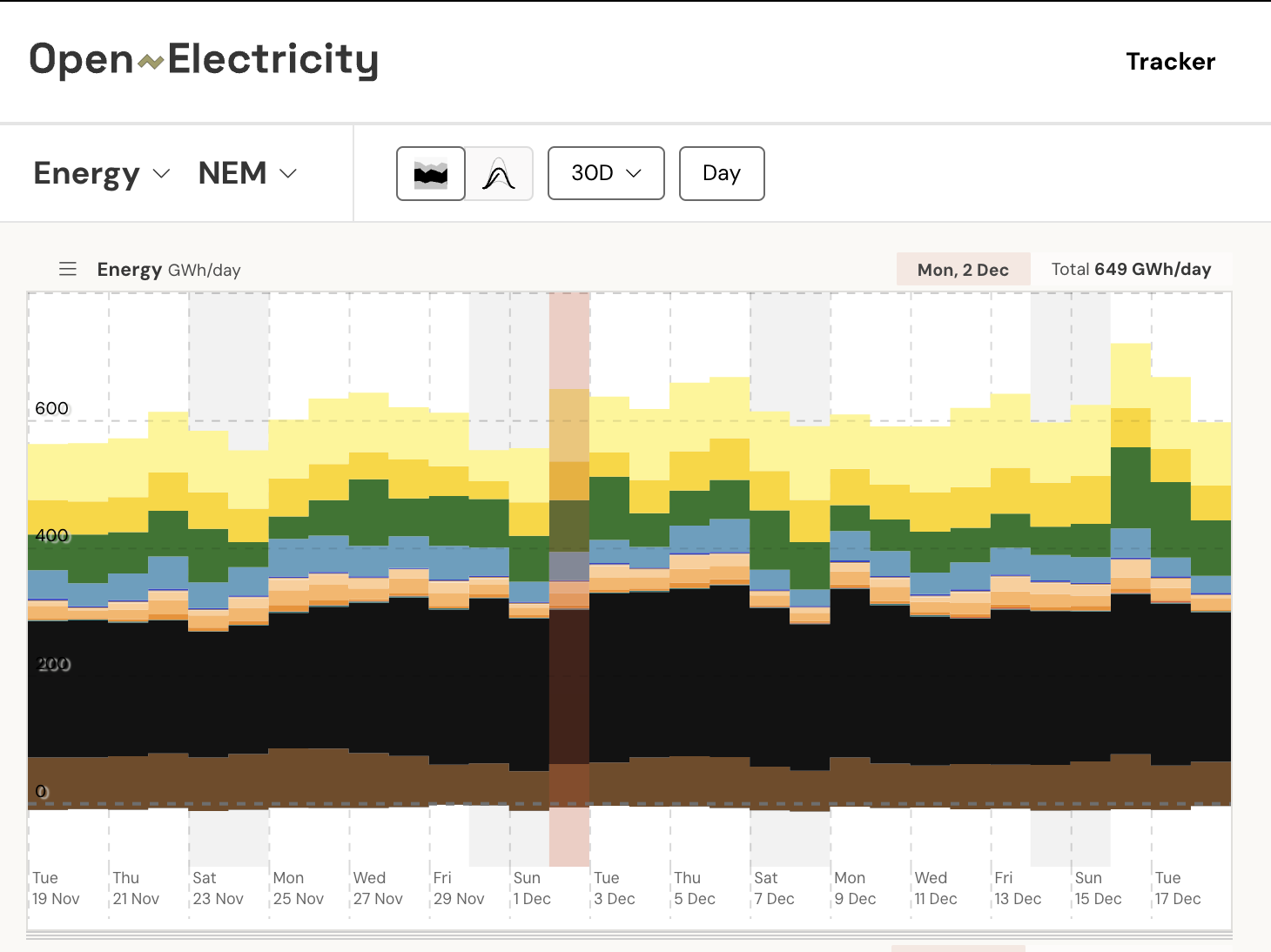
Energy in the context of electricity networks refers to the total amount of electrical power consumed or generated over a specific period. It is typically measured in megawatt-hours (MWh) at facility scale and gigawatt-hours (GWh) at network and grid scale. Unlike power, which is an instantaneous measurement, energy accounts for the duration over which power is used or produced.

​

Definition of Energy

Energy is the integral of power over time, representing the area under the power curve on a graph of power versus time. In simpler terms, it is the accumulation of power usage or generation over a given time interval. For example, if a device uses 1 kilowatt (kW) of power continuously for one hour, it consumes 1 kilowatt-hour (kWh) of energy.

​

Difference Between Energy and Power

• Power: Power is the rate at which energy is generated or consumed at any given moment. It is an instantaneous measurement and is typically expressed in watts (W) or megawatts (MW).

• Energy: Energy is the total amount of power used or generated over a period of time. It is a cumulative measurement and is expressed in kilowatt-hours (kWh) or megawatt-hours (MWh).

In essence, power is about the rate of energy flow, while energy is about the total amount of energy transferred over time.

​

Energy Calculation in OpenElectricity

OpenElectricity calculates energy for each interval by averaging the power generated during that interval and the previous interval. This method provides a more accurate representation of energy usage or generation over time.

​

Calculation Method

The energy for a given interval is calculated using the following formula:

Where:

$E_i: \text{Energy during the interval (in MWh).} \\[8pt]$ $P_i: \text{Power during the current interval } i \text{ (in MW).} \\[8pt]$ $P_{i-1}: \text{Power during the previous interval } i-1 \text{ (in MW).} \\[8pt]$ $\Delta t: \text{Duration of the interval in hours (e.g., for 5 minutes, } \Delta t = \frac{1}{12} \text{).} \\[8pt]$

​

Calculation Example

Calculate the energy for a 5-minute interval where the power during the current interval is 60 MW and the power during the previous interval is 50 MW.

$P_i = 60 \, \text{MW} \, (\text{power during the current interval})$

$P_{i-1} = 50 \, \text{MW} \, (\text{power during the previous interval})$

$\Delta t = \frac{1}{12} \, \text{hours} \, (\text{5-minute interval})$

Step 1: Average the Power Values

$\text{Average Power} = \frac{P_i + P_{i-1}}{2} = \frac{60 + 50}{2} = 55 \, \text{MW}$

Step 2: Divide by Interval Duration

$\text{Energy} = \text{Average Power} \times \Delta t = 55 \, \text{MW} \times \frac{1}{12} \, \text{hours} = 4.583 \, \text{MWh}$

We get a result that is 4.583 MWh, the energy in MWh for that 5-minute interval.